Tests of rating variations on the CFC ratings database
March, 2010
R. Patterson
A) Executive Summary
A program was written to rerate CFC tournament data using an arbitrary rating function. Motivation for doing this was
· previous modifications of the rating system were done without analysis of the effects. This provides a demonstration of one tool that can be used to provide data prior to modifications being approved and implemented.
· concerns that some of the previous modifications to the rating system, in particular the Stockhausen bonus points were having undesired effects.
· concerns that underrated juniors were a problem in the rating pool and that a more directed bonus point system would be an improvement on the existing rating system.
· concerns over possible inflationary aspects of the rating system and a lack of tools to analyze them.
The existing tournament data from Jan. 2006 to Sept. 2011 was used under various rating formulae to look at the CFC rating system. It is the conclusion of the author that, for this data set:
· the CFC rating system without any bonus or participation points is deflationary. Some injection of rating points is required although how many is not particularly clear and the point is arguable.
· The Stockhausen bonus points seemed to have been captured by a small group of high rated players resulting in individual rating inflation detrimental to the rating system.
· a proposed bonus point system does a superior job of injecting rating points. In this context, "superior" means resulting in a lower RMSE (root mean square error) for the predictions of results by the rating system.
One important caveat to all of this is that the population of rated players in the system is currently changing dramatically as many juniors are being transferred to the Quick rating system. This may substantially affect deflationary pressures in the system and may have other effects.
B) Introduction
For the data period considered, January 2006 to September 2011, the CFC has used a number of modifications to the standard rating system. These include:
· a one time bonus based on participation to counter perceived rating deflation. (here after referred to as the Hamilton bonus) At the time, this was criticized for both the lack of rigour in showing that deflation existed and for the erratic nature of how the bonus was distributed among players in a manner that did not reflect playing strength.
· a participation bonus that varied strongly by rating level (ranging from 2 to 0.5 points per game). This was eventually removed. From a technical viewpoint the participation bonus has some undesirable aspects: a) participation points dependent on rating changes the shape of the rating distribution curve (i.e. moves lower rated players closer to higher rated players than would be warranted by the rating formula) and b) participation points potentially introduces regional disparities in inflation due to varying regional participation rates.
· introduced at the same time as the participation bonus and still used in the system, a bonus dependent on achieving at least 60% score in a tournament and having a performance rating higher than the personal best rating (here after referred to as the Stockhausen bonus). Objections to this bonus include:
o The formula and bonus awarded is not based on any mathematical principle or system analysis but is a "made up" formula without any underlying justification.
o The bonus is not scaled by the K factor (currently, for players over 2200, ratings are adjusted at half the rated of U2200 players with the exception of the Stockhausen bonus). This exacerbates the effect of the bonus on over 2200 players.
o after the introduction of the bonus, the ratings of some specific players reached what some considered unreasonable levels (e.g. Sambuev reaching a rating of 2750).
Concerns that the CFC has implemented changes to the rating system without sufficient knowledge, understanding, or data and that the database itself is an underused repository of knowledge that could be better utilized have led me to undertake various data mining efforts and to develop a program that can rerate the database using an arbitrary rating formula.
In particular, the current rating auditor has been concerned about the effects of the Stockhausen bonus and apparently related rating anomalies as well as wishing to do something about perceived underrating of improving juniors. Work has been done to look at these issues resulting in the proposal in this document to change the bonus system.
C) Methodology
1. Regressions were run against the CFC data for individual ratings against rating either a year later or a fixed number of games later in order to identify variables that might be useful in constructing a bonus point system. Although the set of people who have increased ratings at a later point in time includes those who have simply improved, it also includes the set of people who were simply initially underrated. Variables determined to be significant were:
a. whether the rating gain in the last tournament was "large"
b. whether the person was reaching a new personal rating high
c. whether the person was a junior.
2. The CFC rating program was reviewed in detail to ensure that modeling matched the actual program. This resulted in a recent correction to the CFC Handbook to ensure that the description in the Handbook accurately matches the program. Also, a few errors in the program were corrected
3. A separate program was written to perform a rerating of the CFC database with an arbitrary rating function.
4. A separate routine was written to calculate the RMSE (Root Mean Square Error) of the rating database to use as a metric to determine whether any particular rating formula was superior to another or not. This methodology (RSME) has been used before in this application, notably a competition held recently documented on ChessBase to find new formulations for FIDE.
5. A variety of formulas using the variables from (1) were generated and cycled through (3) and (4) for evaluation.
We did not consider formulations that would award negative "bonus points" for unusually bad performances.
D) Caveats:
1. The CFC rating program handles tournaments with greater than 50% unrated players by asking for human input (an estimated average rating as determined by the operator). As such, this is not a deterministic formula and cannot be replicated by any program. My program does not rate these tournaments. As a rule, such tournaments are usually low level junior tournaments, many of whom never play again. Something like 20% of low level junior tournaments are in this category. Consequently, of the roughly 12,700 people who played rated games in this period, roughly 3400 of those people are not rated in my program. In the actual CFC data, these people's ratings are primarily affected by the rating input by the operator rather than by a pure calculation.
2. Currently, many of the junior events that have been rated under the regular rating system are being moved to the Quick chess rating system. As such, the population on which the data analysis is based on for 2006-2011 will be much different in the future and the analysis may be different for whatever the new population looks like. Approximately 50% of the games in the system involve low rated junior tournaments, most of which will not be rated in the regular system in the future.
3. If juniors start in the Quick rating system before graduating to the regular rating system, they will enter the regular rating system at higher strength and probably have a different impact on deflationary aspects of the rating system.
4. It is not clear what time constants are present in the system; e.g. if bonus points are given preferentially to one group say players rated 1200-1600 how long it takes before that affects players in some other group say >2200. Possibly the time period studied is short compared to some of the system time constants.
5. It is impossible to say if the operator input for tournaments with a high percentage of unrated players is systematically biased and what it's effects are.
E) Ratings Inflation:
Comparing the results of different rating models on the same game dataset makes it possible to make statements about the relative effects of the models on ratings inflation on the same dataset. However, there are some limitations on such analysis:
1. It is only possible to compare relative levels of inflation. Determination of the "right" level of inflation requires an external judgment.
2. There is no one measure of inflation to compare rating levels. For example one could use the median rating, the average rating, the median rating of the top 100 players, the average rating of the top 100 players and they all give different answers.
3. The past is no guarantee of the future. What ever happened in the current data set is not guaranteed to reoccur in the future. In particular, the composition of the players in the current dataset is changing rapidly for the future as low level junior tournaments are transitioned out of the regular rating system.
F) Proposed Model
A large number of models were considered and evaluated primarily with a view of lowering the system RSME to arrive at a reasonable set of bonus parameters. The final model that is being proposed is:
![]()
where:
a = 1 if the new rating is at an all time
high, 0 otherwise;
![]() ;
;
n is the number of games played (the
functional dependence is chosen to be consistent with statistical theory on
random walks);
Keff is the ratio of the
player's K factor to the K factor used for 1500 rated players;
Rnew is his new rating and Rold
is pre-tournament rating;
and RatingMaxBonus, RtgChangeBonus, and
RtgChangeThreshold are constants.
That is, the player receives a bonus of
RatingMaxBonus if he is at an all time high plus RtgChangBonus for every point
he gained over a threshold value with everything scaled to reflect the K factor
used for his rating group.
The values chosen for the constants (after
modeling many different values) are:
RatingMaxBonus = 20; RtgChangeBonus =
1.75; RtgChangeThreshold = 13
In separate tests of both components of
the bonus (i.e. one component for reaching a lifetime high, one for exceeding a
threshold rating gain), both were independently necessary for lowering the RSME.
The significant variable of the person's
age was not included because of two reasons:
1.
The CFC database is erratic in it's
recording of player birthdate
2.
A bonus based on a player's age, although
possibly a good predictor, would mean that the rating system depends on factors
other than the ability to play a certain level of chess.
G) Results
Table 1 shows mean and average ratings for a variety of scenarios. Included in the means are only those who a) played at least one rated game in the dataset and b) received a non zero rating in the calculations (as noted previously, this is about 9300 people out of the total of 12,700 in the dataset).
By way of comparison, a graph of the historical average rating of the top 100 can be found at: http://www.victoriachess.com/cfc/ranking_analysis.php . Note the comparisons in the table involve the same players having played the same games whereas the numbers in the link involve different players at each point (because some people quit, joined, etc.).
In this table, column A is the actual CFC rating result. Bear in mind that this includes all of the changes to the rating system that the CFC has implemented e.g. Hamilton bonus, participation points, Stockhausen bonus as well as the effects of the errors that were corrected in the rating program.
Column C is approximately speaking a calculation using the rules in place now, i.e. with a Stockhausen bonus but no other bonuses.
Column D is a calculation without any bonuses at all.
Options 1 is presented as bonus scheme for consideration with parameters as previously specified.
RMSE is the Root Mean Square Error of the system. Lower values are better.
Table 1 Average and Mean Ratings
|
A |
C |
D |
Option
1 |
|
|
Average |
1189 |
1080 |
1068 |
1143 |
|
Median |
1112 |
966 |
950 |
1047 |
|
top 100 Canadian average |
2391 |
2323 |
2295 |
2368 |
|
top 100 Canadian median |
2361 |
2309 |
2290 |
2334 |
|
RMSE |
0.413015 |
0.413983 |
0.408389 |
From a relative inflation perspective, comparing columns A and D in table 2, it can be seen that the various rating point injections done in the CFC system amount to a relative inflation of 70-160 points depending on the chosenmeasure of inflation. It is also apparent that Options 1 (as well as Column C) are somewhere in between these possibilities.
Table 2 Relative inflation: CFC to no bonus points
|
A-D |
|
|
Average |
121 |
|
Median |
162 |
|
top 100 Canadian average |
96 |
|
top 100 Canadian median |
71 |
H) Case Studies:
Relying solely on the RMSE as a guide for model selection can be misleading. Options that lower the RMSE can have unexpected effects that may outweigh any benefits of the bonus scheme per se. As an example, consider the Stockhausen bonus (column C) versus no bonus (Column D). Nominally it has a lower RMSE but it is also connected (at least anecdotally) with the overshoot of some players' ratings at the top level (e.g. Sambuev). To aid in viewing what effects the two options presented may have, a number of rating graphs for Case Studies of particular players are presented (at the end of this paper).
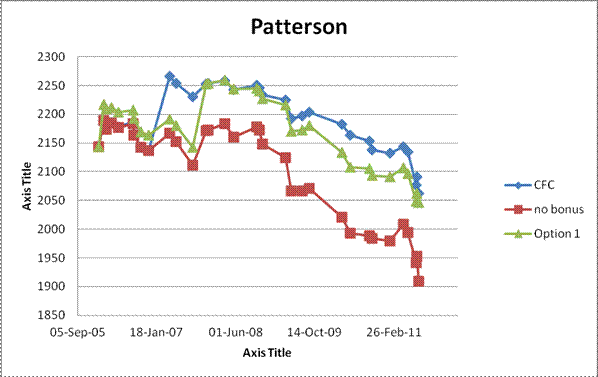
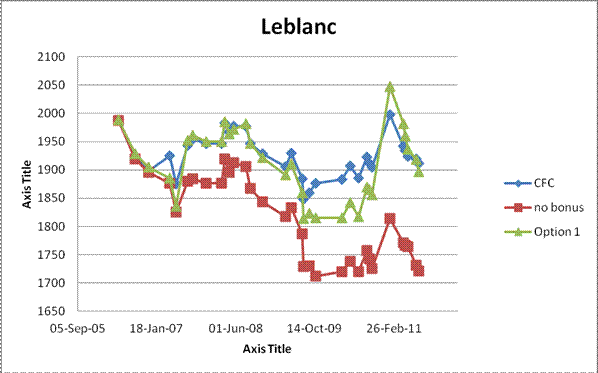
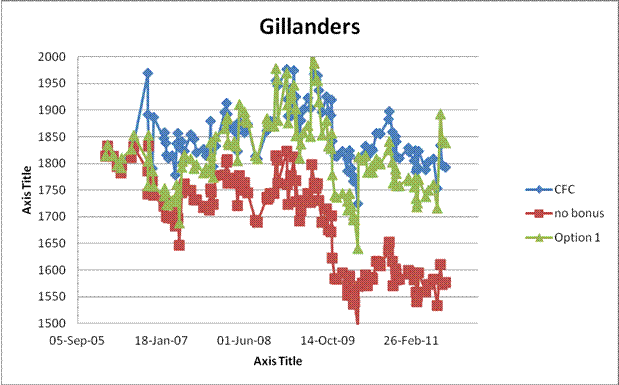
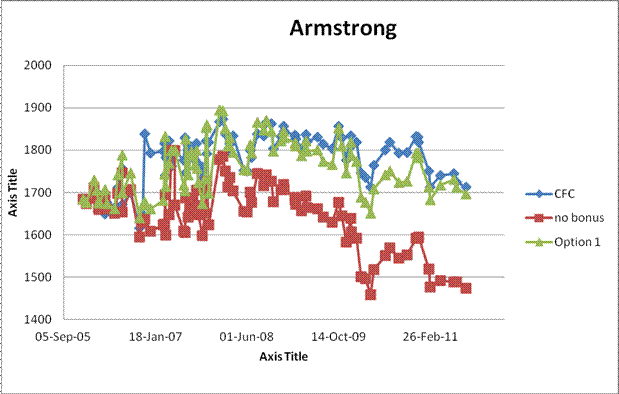
Group 1: Players of a certain age who would be expected to be stable or perhaps slowly declining: R. Patterson, P. Leblanc, R. Gillanders, R. Armstrong.
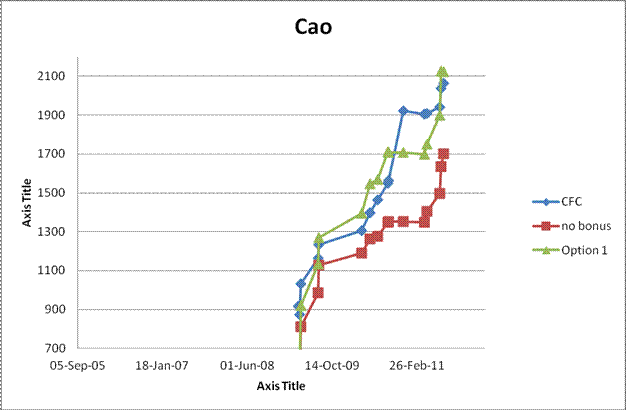
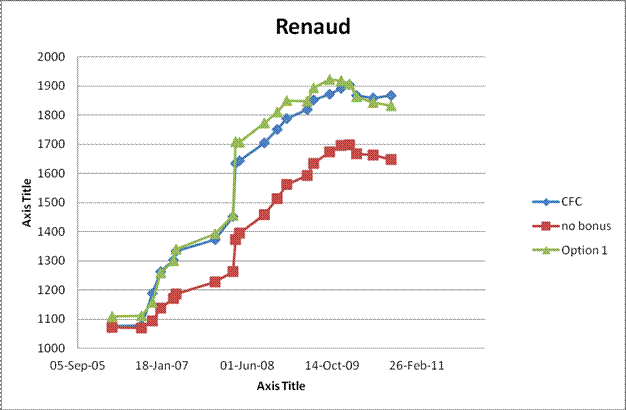
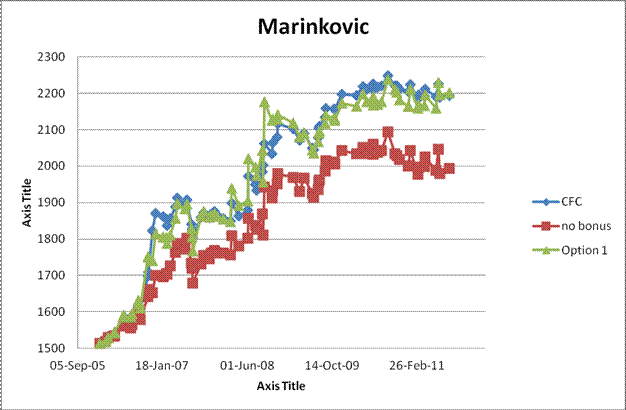
Group 2: Rapidly improving juniors who nominally would be expected to be frequently underrated and hopefully benefit most from the bonus scheme: J. Cao (U10 2010 Word Champion), J. Renaud (someone who has had 28 tournaments in a row resulting in a rating increase), M. Marinkovic (a very active junior).
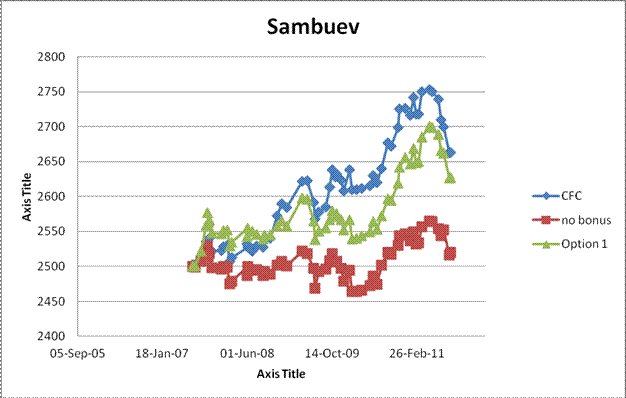
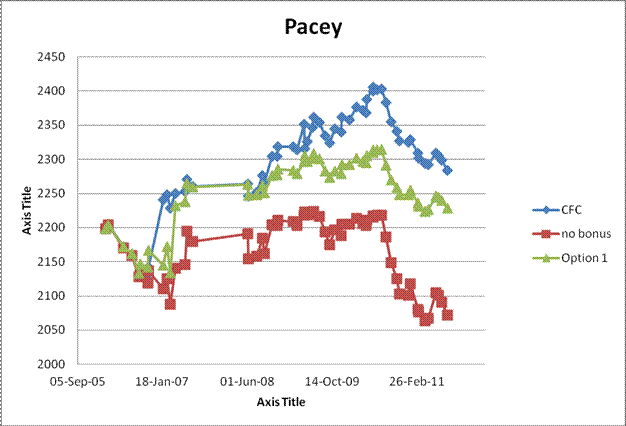
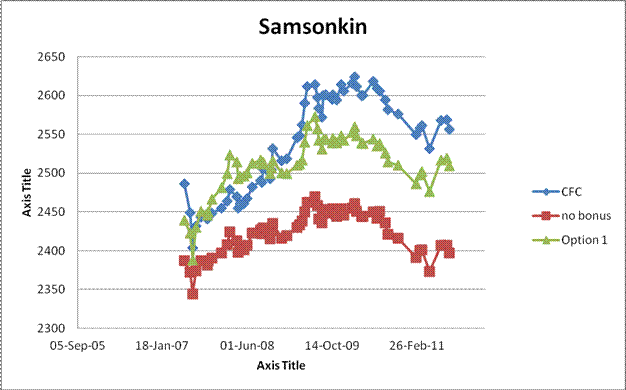
Group 3: Players suspected to have overly benefited from the Stockhausen bonus.: B. Sambuev (reached 2750), K Pacey (although in early 50's, sprinted roughly 150 points to reach a personal lifetime high of 2400), A. Samsokin (selected more or less at random from a group of high rated Ontario players)
Looking at the rating graphs for group 1, there is not a lot to choose from between the existing CFC ratings and those of Option 1. Option 1 is a little lower and perhaps a bit more volatile but is quite similar and reasonably stable. On the other hand, it is hard to avoid the impression that the "no bonus" condition is strongly deflationary.
In the graphs for group 2, recall that the CFC gave Cao a one time bonus of about 350 points after his World Championship victory. Absent that, his CFC rating here would top out somewhere between 1900 and 2000, well below his recent playing strength. Option 1 is for most of his career about 150 points higher than the CFC rating (hard to tell from the graph because of the vertical scale) so it does succeed in directing points to his rating. From personal experience, I would say this is certainly closer to his strength in that period. Note that the flat part in his rating curve corresponds to a sequence of junior tournaments in which he scored 14.5/15. That he did not gain rating points says more about the quality of the opposition than it does about his rating. Renaud's graph (chosen because of his string of 28 consecutive rating increases in the CFC system) also shows Option 1 giving him a higher rating during the time of his improvement (about 70 points). On the other hand, a very active junior such as Marinkovic (419 games compared to ~90-95 for the other two) shows little difference between the existing CFC and Option 1. If the junior is active enough, his rating will keep up. In all three cases, the rating curve without bonuses is clearly insufficient (although possibly tied up with a general deflation).
The third group of graphs, for people suspected to have overly benefited from the Stockhausen bonus, show a clear divergence of about 50-100 points of the CFC rating over the Option presented during the time frame that the Stockhausen bonus (and participation points) was implemented. It seems fairly clear that the CFC rating is too high (compare for example to FIDE ratings. A 2750 rating is high up in the world rankings). I have not examined these cases in detail but believe the basic problems are:
1. The Stockhausen bonus is not scaled for the reduced K factor at these ratings.
2. The Stockhausen bonus is too easy to get at these ratings (requiring only that the player's performance rating be higher than the player's highest rating - a roughly 50% chance.)
3. It may also be possible that a small group of players repeatedly playing each other and repeatedly getting a Stockhausen bonus caused a localized inflation.
Although it seems clear the CFC rating is too high, it is not clear what the correct level is or even that the "no bonus" calculation does not give correct ratings. Sambuev for example, clearly did have a "good run" of results so where should his rating have ended up?
The bonus scheme proposed is open to the same possible sequence (repeatedly getting the bonus for being at a personal high) but is significantly rarer in application and harder to get (as well as being scaled by the K factor).
Seeing as an important role of the rating system at the high levels is its use as a selection tool for national events and consequently stability of high level ratings is an important factor it might be wise to eliminate all bonuses above a certain level, say 2400.
I) Summary
For the dataset examined, the rating system without any bonuses is deflationary. The existing set of bonus and participation points is however deficient in that it does not really affect the ratings of up and coming juniors and seems to have had some deleterious effects for some high rated players.
A bonus scheme is proposed and examined that is based on parameters found to be statistically significant in predicting higher individual ratings. It is an improvement on the existing system in the sense that it provides a lower Root Mean Square Error for the dataset.